La suite de Fibonacci – Design et proportion – une spirale montre le chemin

Leonardo Fibonacci

Il y a environ 800 ans, l'Italien Leonardo Pisano (1170-1240), mieux connu sous le nom de Leonardo Fibonacci, apprit lors de ses voyages autour de la Méditerranée l’ensemble des mathématiques de son époque. Il écrivit le livre « Liber Abaci ». Grâce à cet ouvrage, il diffusa au 13e siècle le système numérique indo-arabe en Europe. Dans ce livre, il mentionne pour la première fois la suite de Fibonacci. Il a calculé le taux de reproduction des lapins et le secret particulier du processus de croissance dans la nature. Visuellement, la suite de Fibonacci est représentée sous forme de spirale – la Spirale dorée.

Le calcul de l'harmonie

La suite de Fibonacci suit une règle simple. Chaque nombre est la somme des deux précédents. Son origine commence par 1. La croissance des nombres augmente rapidement au fur et à mesure que la suite progresse.

1 + 1 = 2
1 + 2 = 3
2 + 3 = 5
3 + 5 = 8
5 + 8 = 13
8 + 13 = 21
13 + 21 = 34
21 + 34 = 55
34 + 55 = 89
55 + 89 = 144

Comment construire la Spirale dorée avec les nombres de Fibonacci ?

La base de la construction est une grille de carrés alignés, dont les côtés suivent la suite de Fibonacci. Les segments de cercle formés dans ces carrés se rejoignent pour créer la spirale de Fibonacci. Cette spirale s'ouvre de plus en plus car la croissance des nombres s'accélère rapidement. Avec un peu d’imagination, on peut y voir une connexion avec la nature. Vois-tu l'escargot ?

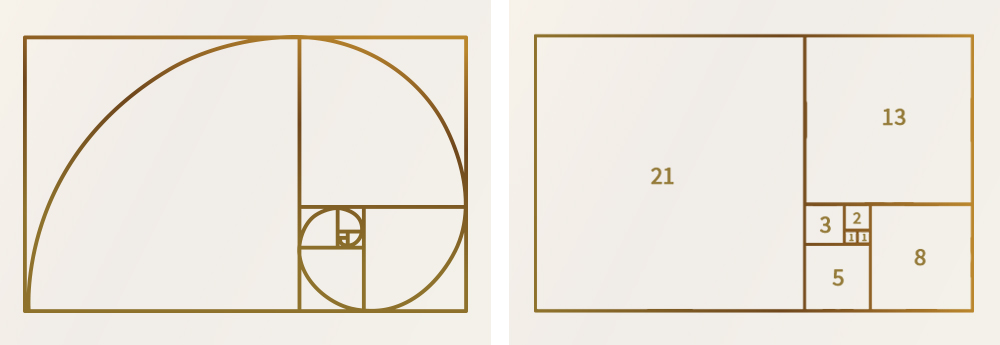
Les nombres de Fibonacci et le nombre d’or sont liés

Si nous simplifions la grille du dessin précédent, nous obtenons un carré et un rectangle. Cette répartition des surfaces correspond presque au nombre d’or.

Le nombre d’or désigne le rapport entre deux surfaces ou deux segments. Le rapport entre la plus grande et la plus petite partie est le même que celui entre la totalité et la plus grande partie. En mathématiques, ce rapport est représenté par le nombre Phi 1,618.

Comment construit-on le nombre d’or ?

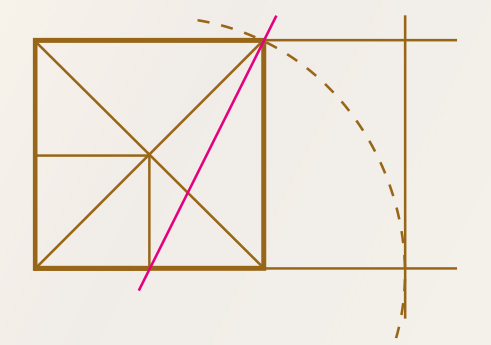
Pour diviser une surface selon le nombre d’or, voici un exemple. Il en existe bien sûr beaucoup d’autres.

À quoi servent les nombres de Fibonacci et le nombre d’or ?

Suite de Fibonacci

La suite de Fibonacci découle du même principe que le nombre d’or. Tous deux décrivent des processus de croissance dans la nature. Regarde, par exemple, les spirales tournant à gauche et à droite sur une pomme de pin, un cactus ou un tournesol. Elles sont en rapport de 8 à 13 ou de 21 à 34 (nombres de la suite de Fibonacci).

Chaque graine de tournesol appartient à une spirale tournant à gauche et à une autre tournant à droite. Le nombre de spirales est toujours un nombre de la suite de Fibonacci.

Dans un tournesol, il existe toujours des combinaisons de spirales de 21/34, 34/55, 55/89 et, dans de grands tournesols, de 89/144 graines.

Si tu divises ces nombres entre eux, le résultat est toujours 1,618, (« Phi » ou le nombre d’or).

Nombre d’or

Dès l'Antiquité, les proportions basées sur le nombre d’or étaient considérées comme belles et esthétiques. Elles se basent sur l'égalité des proportions. Partout où il est question de proportions et d'une répartition harmonieuse, nous utilisons ces calculs.

Le plus connu est le miroir de page. C’est ainsi que l’on appelle la répartition des marges dans les livres, brochures et magazines. Tous les écarts et dimensions pour les marges, les espacements entre les colonnes ou les lignes sont calculés sur la base de ces formules. Il s'agit du rapport entre la zone imprimée et l'espace blanc.

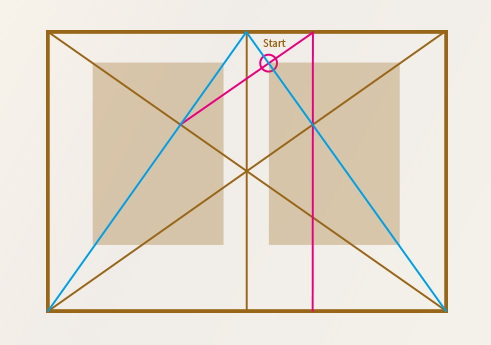
En photographie et en peinture, tu peux également influencer l'effet visuel d’une image en appliquant ces principes de composition.

Exemple : Si tu places ton sujet principal au centre de la spirale, ton image aura une apparence harmonieuse et équilibrée.